What are FDatas?#
In the previous section we ended by noting a download that happened as we tried to compute the energies for our example. This download is requiered as we need what we call FDatas.
So, what is a FData? It is the collection of precomputed
integrals of the base functions which allow for massive
speed improvement as they do not need to be calculated every time.
In exchange, it does occupy space in the hard disk (few hundred MBs)
and requiere a download the first time they are used.
You can check what FDatas are available by using the
available_fdatas() function.
Before moving further we should address the question:
“Are you downloading files into my computer?” Yes.
We aknowledge the posible security concerns which is why
we perform sha256sum checks to ensure nothing wrong
happens with the download.
We also ask before updating any FData and replacing files.
Nonetheless, this a good time as any to remind that no
script (ours or not) should EVER be executed with administrator
priviledges unless you place the utmost trust on it and it is strictly necessary.
To end with this discourse, you may check where these files
are downloaded with the get_fb_home() function.
The download path may be controlled with the environmental variable
FIREBALL_HOME. By default it will take the path
given by the environmental variable XDG_CACHE_HOME or
fallback to the Unix default ~/.cache/.
The next question one may have is what FData to use. We have prepared a whole set of FDatas available to be fetched from FireballPy. Find a brief summary of them in the next table:
If you find that no FData may suit your need please feel free to contact us!
After this gentle introduction to the concept of FDatas is time to return to coding and explore the nice things FireballPy can do!
Whow to do FDatas?#
If you want to construct an fdata, the first thing you need is the wavefunctions for the orbitals of the atoms you require and the pseudopotentials. The fdata command will automatically obtain them from here.
If you want to generate the wavefunctions yourself, you can do so using the fdata command, which should have been installed when you installed fireballpy. For example, let’s generate the (sp) orbitals for a Si atom:
fdata wavefunctions --element N --orbitals spd -n 2.00 3.00 0.00 -r 5.00 5.00 5.00
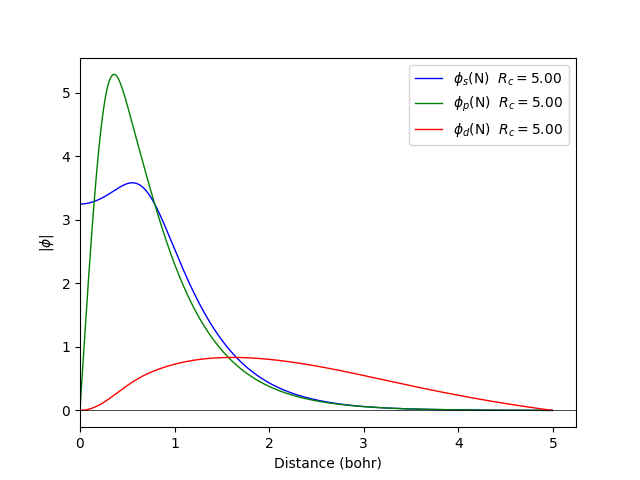
We can compress the orbitals using a confining potential. In the following example, we will apply it only to the d orbital:
fdata wavefunctions --element N --orbitals spd -n 2.00 3.00 0.00 -r 5.00 5.00 5.00 --vpot 0.00 0.00 20.00 --rpot 0.00 0.00 2.00
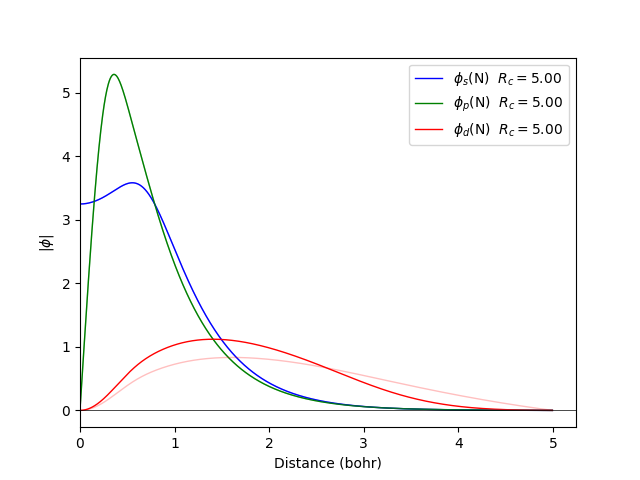
Another way to modify the shape of the orbitals is to generate them with less charge:
fdata wavefunctions --element N --orbitals spd -n 0.00 0.00 0.00 -r 5.00 5.00 5.00
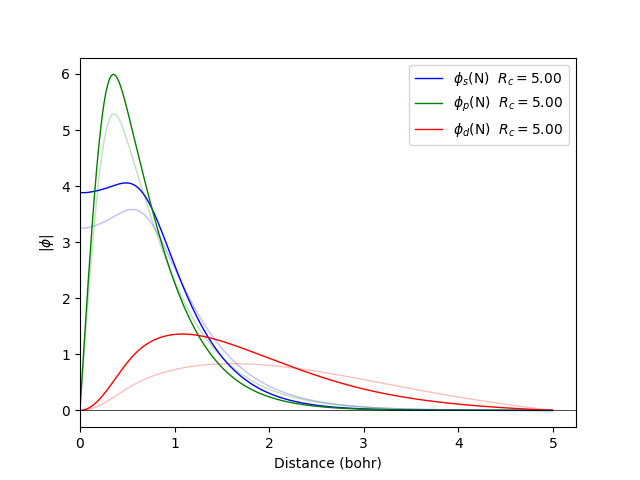
Even though the atom remains neutral, meaning that the neutral atom and charged atom potentials (i.e., Hartree interactions) are generated. The neutral atom potential is determined from:
The charged atom potential is based on the wavefunction of the shell, so the piece for the s-shell is determined by:
These Hartree potentials are required for calculating Coulombic shell potentials when solving the one-electron Schrödinger equation.
A set of slightly excited pseudo-atomic Fireball wavefunctions are computed within density-functional theory (using either the local-density approximation or generalized gradient corrections) and a norm-conserving separable pseudo-potential [FS99] . These wavefunctions are chosen such that they smoothly vanish at the cutoff radius. These pseudopotentials will also be downloaded automatically from here.
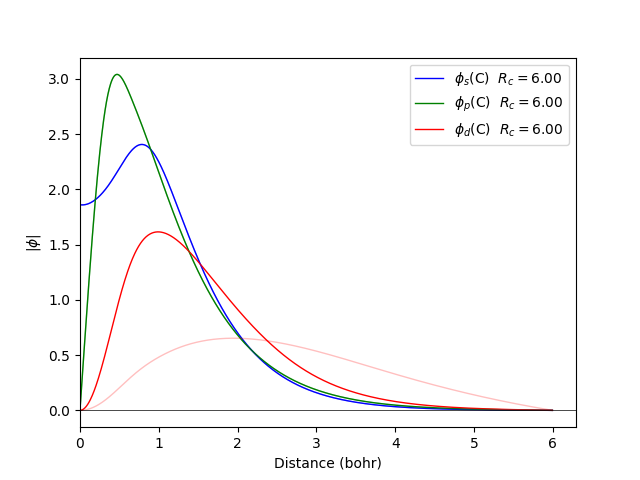
We can mix orbitals from different calculations. For example, we use charges of 2.0 and 0.2 for the sp orbitals, while for the d orbitals we use 0.0 0.0 0.0.
fdata wavefunctions --element C --orbitals spd -n 2.00 0.20 0.0 -r 6.00 6.00 6.00 --save sp
fdata wavefunctions --element C --orbitals spd -n 0.00 0.00 0.0 -r 6.00 6.00 6.00 --save d
fdata wavefunctions finnish C -o cinput
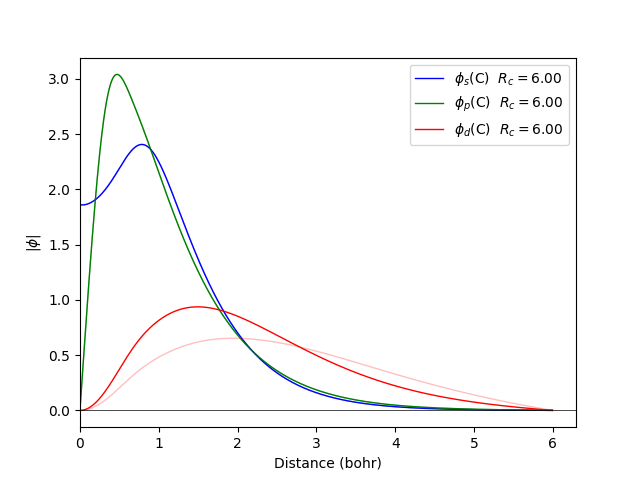
Another way to mix orbital calculations is by modifying the charge in the pseudopotential to generate the d orbital.
fdata wavefunctions --element C --orbitals spd -n 2.00 0.20 0.0 -r 6.00 6.00 6.00 --save sp
fdata wavefunctions --element C --orbitals spd -n 2.00 0.20 0.0 -r 6.00 6.00 6.00 --valence-pp 7.00 --save d
fdata wavefunctions finnish C -o cinput
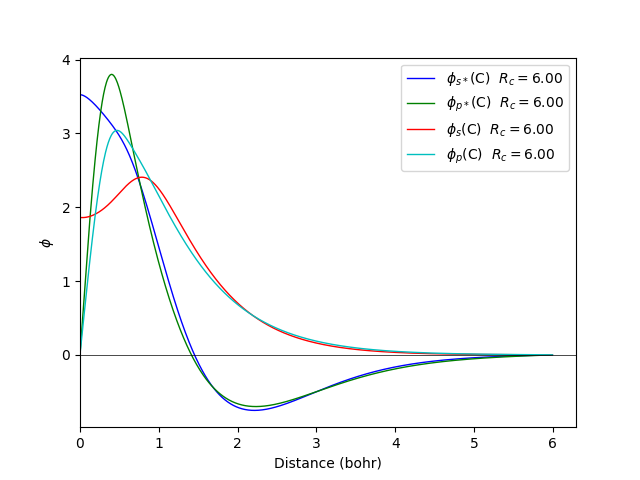
To generate orbitals by using the mixing factor, optimized wavefunctions mixing ground state and excited states
fdata wavefunctions --element H --orbitals s --excite mix -n 1.0 --pmix <pmix> --nion 1.00 -r 4.00

If we want to obtain excited-state orbitals using the DMOL option, we execute the command:
fdata wavefunctions --element C --excite DMOL --orbitals sp -n 2.00 0.20 --nion 0.00 0.00 -r 6.00 6.00
References#
Martin Fuchs and Matthias Scheffler. Ab initio pseudopotentials for electronic structure calculations of poly-atomic systems using density-functional theory. Computer Physics Communications, 119(1):67–98, 1999. URL: https://www.sciencedirect.com/science/article/pii/S001046559800201X, doi:https://doi.org/10.1016/S0010-4655(98)00201-X.